基于图像的照明（IBL）技术

基于图像的照明（Image-Based Lighting，以下简称 IBL）是一种在实时图形与物理渲染中广泛应用的环境光照技术，其研究起源可以追溯到 1998 年 Paul Debevec 的开创性工作 。该技术通过对整个场景或某一局部空间的实际光照环境进行图像捕捉，并将该图像用于计算物体表面受到的间接光照影响，从而实现更加自然与真实的渲染效果。IBL 不再依赖传统的点光源、平行光等显式光源模型，而是借助环境贴图（Environment Map）这一全景光照数据，实现对全局光照的模拟，尤其在渲染复杂材质（如金属、高光表面）时具有明显优势。

在实际应用中，IBL 通常使用球形环境贴图（Spherical Environment Map）或立方体贴图（Cubemap）来存储捕捉到的环境光照图像。这些贴图可以来源于真实世界中的场景采样（如 HDR 全景照片），也可以通过预渲染方式合成得到。在 PBR 系统中，IBL 一般同时用于计算材质的漫反射与镜面反射部分。为了保证渲染器在运行时的速度，IBL 技术会预计算多项参数，存储在纹理中，在运行时通过采样纹理的方式获得需要的参数。在漫反射部分，IBL 的实现通常通过对环境贴图进行重要性采样，计算出环境贴图出球面谐波函数参数，在实时渲染时使用球面谐波函数计算漫反射项。而在镜面反射部分，则利用预滤波（Prefiltered Environment Map）与 BRDF 积分查找表（BRDF LUT）共同完成模拟。预滤波环境贴图将不同粗糙度下的镜面反射分布预先编码为多级 Mipmap，而 BRDF LUT 则用于在实时运行时快速查找不同粗糙度和观察角度下的 Fresnel 和几何遮蔽影响因子。通过这些预处理资源的配合，IBL 能在保证物理准确性的同时，显著降低实时计算的复杂度。

实时渲染中的 IBL

真正让 IBL 在实时渲染成为可能，使其成为实时渲染标准的是 Brian Karis 的优化方案。Brian Karis 引入了辐照度预滤波和 BRDF 预积分的方法，使得 IBL 在运行时到速度达到了实时渲染可以接受的范围（见 Real Shading in Unreal Engine 4 ）。在 IBL 的计算过程中，仍然使用 Cook-Torrance 微表面模型理论，也会将漫反射项与镜面反射项分开计算。

在漫反射计算中，我们通过球面谐波（Spherical Harmonics, SH）进行逼近。具体来说，我们会在预处理阶段，将环境光照分布表示为一组球面谐波基函数的线性组合。由于漫反射只关心入射光与表面法线之间的夹角，并且这种依赖关系在半球范围内是平滑变化的，因此可以利用较低阶的球面谐波基函数准确描述。通常使用二阶的球面谐波函数来描述环境贴图的漫反射信息。

在镜面反射计算中，实时渲染通常使用 Brian Karis 的 Split Sum Approximation 方法（见 Real Shading in Unreal Engine 4 ）。此方法将大部分计算工作转移到了预处理阶段，并将结果存储在显存中，极大减少了运行时的计算量。其公式如下：

在 Split Sum Approximation 中，渲染方程中的镜面反射项被近似拆分为可以独立预计算的两部分：第一部分描述了在不同粗糙度条件下，来自所有入射方向的环境光对表面反射贡献的累积，即对环境贴图进行模糊卷积后得到的预滤波结果；第二部分则表示与表面材质相关的 BRDF 与几何项、菲涅尔项的积分结果，通常预计算为一个仅依赖于粗糙度与视角角度的查找表（LUT）。该拆分将高维积分转化为两次低维查询，有良好的实时性能的同时保证了不错的视觉效果，并近似保持了能量守恒和微表面散射特性。

IBL 在 Wgpu 与 Rust 中的实现

在 IBL 的实现部分，本软件会在导入环境贴图后进行三个部分的预处理。分别是HDRI 环境贴图到 Cubemap 转换、漫反射项会用到的球面谐波函数参数的预计算，以及镜面反射项会用到的环境贴图的预滤波。

HDRI 到 Cubemap 转换

通常环境贴图以 HDRI（高动态范围图像）存储。要想让高动态范围颜色在 Wgpu 中被正确表达，本软件使用格式为 Float16 的颜色格式在显存中存储高动态范围图像，这意味着每个通道使用一个 16 位浮点数来表达。除此之外，HDRI 使用球面投影来将一个球面上的贴图投影到平面。但是在实时渲染中，通常会使用 Cubemap （立方体纹理）来存储环境贴图，这有更好的显存利用率和采样速度。所以在导入 HDR 图像作为环境贴图时，本软件会将一张 HDR 图像转换成高动态范围的 Cubemap。

具体到转换的过程，首先软件会使用一个静态的 单位立方体模型 （在软件初始化时既上传到 GPU），其六个面分别对应世界坐标系的正负轴向（+X、-X、+Y、-Y、+Z、-Z）。每个面需要配置独立的视图矩阵与正交投影矩阵，以定义从立方体中心到各面的观察方向与投影范围。例如+X面的视图矩阵将相机看向+X方向，正交投影的视锥范围定义为近平面0.1、远平面10.0，覆盖立方体面的尺寸。其余五个面以此类推，通过调整视图矩阵的 look_at 参数和投影矩阵的左右上下边界实现。

接着在渲染管线中顶点着色器负责将立方体顶点转换到世界空间，片元着色器则根据当前渲染的面方向，从 HDR 全景图中采样对应区域的光照数据。关键代码逻辑如下：

// 空间方向到平面坐标
fn sample_spherical_map(dir: vec3<f32>) -> vec2<f32> {
    let phi = atan2(dir.z, dir.x);
    let theta = acos(clamp(dir.y, -1.0, 1.0));
    let uv = vec2<f32>(phi / (2.0 * PI) + 0.5, theta / PI);
    return uv;
}
...
    // 片源着色器主程序
    let uv = sample_spherical_map(normalize(in.local_position));
    let color = textureSample(tex, samp, uv);
    return vec4<f32>(color.xyz, 1.0);

因为在 Wgpu 中，Cubemap 实质上是六个纹理的数组，同时，因为不能只能渲染到一个 Cubemap 纹理上，所以软件通过多次渲染的方式使用六个不同的变换矩阵进行六次渲染，对应 Cubemap 的每一个面。同时在每次渲染中，软件会为每个纹理创建一个 View，View 是一张纹理的子集的访问信息，它可以限制一张纹理只被访问一小部分，这个纹理作为当前 Pass 的渲染目标。变换矩阵的 BindGroup 已经上传到 GPU 并存储在一个数组中。使用 0 号槽位绑定 Matrix 数组绑定组，1 号槽位绑定 HRD 2D 图像。关键代码逻辑如下：

let ret_texture = device.create_texture(&TextureDescriptor {
    size: wgpu::Extent3d {
        width: piece_size,
        height: piece_size,
        depth_or_array_layers: 6, // Cubemap 的 layers 为 6
    },
    ...
}
...
for i in 0..6 {
    let matrix_bind_group = self.matrix_bind_groups[i];
    let target = ret_texture.create_view(&wgpu::TextureViewDescriptor {
        dimension: Some(wgpu::TextureViewDimension::D2),
        base_array_layer: i as u32,
        array_layer_count: Some(1),
        ..Default::default()
    });
    // 在 Pass 中设置 target View 为目标
    let mut render_pass = encoder.begin_render_pass(...);

    render_pass.set_pipeline(&self.pipeline);
    render_pass.set_vertex_buffer(0, cube_vertex_buffer.slice(..));
    render_pass.set_bind_group(0, matrix_bind_group, &[]);
    render_pass.set_bind_group(1, &texture_bind_group, &[]);
    render_pass.draw(0..36, 0..1)
}

ret_texture 即为转换后的 Cubemap 纹理。

球面谐波函数预计算

在实时 IBL 漫反射计算中，本软件使用二阶的球面谐波函数进行逼近。因此需要预计算出二阶球面谐波函数的九个系数。这些系数记录了环境光在不同方向上的分布特性。

这个预计算发生在 CPU 侧，使用 Rust 完成。因为环境贴图球面投影，因此需要一个转换函数，转换球面投影的二位坐标到三位空间的方向向量：

fn texel_to_dir(x: u32, y: u32, width: u32, height: u32) -> [f32; 3] {
    let u = (x as f32 + 0.5) / width as f32;
    let v = (y as f32 + 0.5) / height as f32;
    let theta = v * PI; // 纬度
    let phi = u * 2.0 * PI; // 经度
    let sin_theta = theta.sin();
    [sin_theta * phi.cos(), theta.cos(), sin_theta * phi.sin()]
}

另外，要预计算球面谐波函数，还需要知道球面谐波函数的九个基函数在某个方向上的值：

fn sh_basis_2nd(dir: [f32; 3]) -> [f32; 9] {
    let (x, y, z) = (dir[0], dir[1], dir[2]);
    [
        0.282095,                       // Y_0_0
        0.488603 * y,                   // Y_1_-1
        0.488603 * z,                   // Y_1_0
        0.488603 * x,                   // Y_1_1
        1.092548 * x * y,               // Y_2_-2
        1.092548 * y * z,               // Y_2_-1
        0.315392 * (3.0 * z * z - 1.0), // Y_2_0
        1.092548 * x * z,               // Y_2_1
        0.546274 * (x * x - y * y),     // Y_2_2
    ]
}

在有了上面两个函数的基础后，软件会根据面积近似，对整张环境贴图进行重要性采样。下面是重要性采样的 Rust 代码：

let mut coeffs = [[0.0f32; 4]; 9]; // 9 个基函数，每个 RGBA
for y in 0..height {
    for x in 0..width {
        let dir = texel_to_dir(x, y, width, height);
        let basis = sh_basis_2nd(dir);
        let (r, g, b) = ...;
        // 球面采样的权重（面积近似）
        let weight = (PI / height as f32) * (2.0 * PI / width as f32) * dir[1].max(0.0); // y=cos(theta)
        for i in 0..9 {
            coeffs[i][0] += r * basis[i] * weight;
            coeffs[i][1] += g * basis[i] * weight;
            coeffs[i][2] += b * basis[i] * weight;
}}}

其中 coeffs 即为代码，之后通过 Wgpu 队列写入缓冲区后就在着色器中被使用。计算好的球面谐波函数系数被用一个 Uniform 缓冲区存储，绑定在全局 BindGroup 中。

预滤波环境贴图

本软件通过基于粗糙度的 GGX 分布卷积生成多级 Mipmap，近似积分微表面法线分布下所有入射光对反射方向的贡献；因为粗糙度越高，滤波后的环境贴图的模糊度越高，频率越低。这种情况下及时将纹理的分辨率降低至原来的一半，采样得到的效果也不会有显著变化。因此本渲染器使用 Mipmap 来存储不同粗糙度下的环境贴图的滤波结果，节约了滤波后的环境贴图的占用的显存空间。笔者希望使用 GPU 进行重要性采样来提升性能，也便于使用既有的 GPU 中的环境贴图，为此需要设定一个特殊的渲染管线，其 BindGroup 绑定的信息包括环境贴图，当次滤波的粗糙度，以及采样的次数。本软件使用了 5 级 Mipmap 来存储滤波后的环境贴图，这个级数已经可以满足效果的需要。与 HDRI 纹理到 Cubemap 的转换过程类似，软件会对六个方向的 Cubemap 纹理进行逐个滤波，并渲染到新的输出纹理当中。在一个 Mipmap 层级的六次渲染中，每次只访问当次需要的 Cubemap 的某个方向的纹理与当前的 Mipmap 级别。也就是说，滤波一张 Cubemap 贴图，需要进行 5 × 6 = 30 次。每次进行渲染，软件都会创建一个临时的 View。由于只需要被采样，所以 View 的用途只需要设置为 RENDER_ATTACHMENT ：

  let target = texture.create_view(&wgpu::TextureViewDescriptor {
      dimension: Some(wgpu::TextureViewDimension::D2),
      usage: Some(wgpu::TextureUsages::RENDER_ATTACHMENT),
      base_mip_level: level, // 当前的 Mipmap 层级
      base_array_layer: j, // 当前的 Cubmap 方向
      ...
  });

Mipmap 级别在软件中用 level 表示。下面为设置渲染管线与 Mipmap 绑定的 Rust 代码：

for level in 1..level_count {
    let roughness = 1.0 / (level_count as f32) * (level as f32);
    ... // 初始化绑定组

    for j in 0..6 {
        let target = ... // 上文提到的新建 View
        let mut pass = encoder.begin_render_pass(&wgpu::RenderPassDescriptor {
            label: Some("Prefiltering"),
            color_attachments: &[Some(wgpu::RenderPassColorAttachment {
                view: &target,
                resolve_target: None,
                ops: wgpu::Operations {
                    load: wgpu::LoadOp::Clear(wgpu::Color::WHITE),
                    store: wgpu::StoreOp::Store,
                },
             ...
        });
        ... // 设置绑定组
        pass.draw(0..36, 0..1); // 绘制立方体
    }
}

queue.submit(std::iter::once(encoder.finish()));

在着色器中，软件使用 Hammersley No Bit 方法生成随机数，来确定某次重要性采样的水平角度和俯仰角度。下面是 Hammersley No Bit 方法的 Wgsl 代码实现。

fn hammersley_no_bit_ops(i: u32, n: u32) -> vec2<f32>{
    return vec2f(f32(i) / f32(n), van_der_corput(i, 2u));
}

软件会在片源着色器中进行重要性采样，使用 作为权重。由于本软件的 GGX 重要性采样的 Wgsl 实现的完整代码较长，其被放在附录中。下面是重要性采样的多次采样部分的 Wgsl 代码：

for (var i: u32 = 0; i < sample_count; i++) {
    let half = importance_sample_ggx(hammersley_no_bit_ops(...), ...);
    let light = normalize(2.0 * dot(view, half) * half - view);
    ...
    if (nDotL > 0.0) {
        color += textureSample(..., light).rgb * nDotL;
        total_weight += nDotL;
    }
}
return color / total_weight;

IBL 实时着色计算

漫反射项的计算通过将这些系数与表面法线方向上对应的球面谐波基函数值相乘并累加完成。下面是本软件在 Wgsl 中使用球面谐波函数计算漫反射项的 Wgsl 代码：

fn irradiance_sh(normal: vec3<f32>) -> vec3<f32>{
    return env_sh_coefficients[0]
    + env_sh_coefficients[1] * (normal.y)
    + env_sh_coefficients[2] * (normal.z)
    + env_sh_coefficients[3] * (normal.x)
    + env_sh_coefficients[4] * (normal.y * normal.x)
    + env_sh_coefficients[5] * (normal.y * normal.z)
    + env_sh_coefficients[6] * (3.0 * normal.z * normal.z - 1.0)
    + env_sh_coefficients[7] * (normal.z * normal.x)
    + env_sh_coefficients[8] * (normal.x * normal.x - normal.y * normal.y);
}
...
let diffuse = diffuse_color * max(irradiance_sh(normal), vec3<f32>(0.0)) / PI;

在获得了 预滤波环境贴图 和 BRDF 预积分 后，经过如下的计算，得到最终的镜面反射项的结果。整体描述计算镜面反射项过程的 Wgsl 代码：

let indirect_specular= evaluate_ibl_spectular(reflect, perceptual_roughness);
let dfg = prefiltered_dfg_lut(perceptual_roughness, nDotV);
let specular_color: vec3<f32> = f0 * dfg.x + f90 * dfg.y;
let specular = indirect_specular * specular_color;

IBL 的结果与前面微表面模型的光照计算的返回值一样，分成漫反射项和镜面反射项返回。

效果截图

透明渲染实现

导入时的透明物体与非透明物体管理

在导入模型时，识别透明物体和非透明物体十分重要，因为不透明物体采样延迟渲染管线渲染，其有更好的渲染效率。许多三维软件并不能高度自定义导出时所有物体的透明度标签。所以很多时候，一个模型文件中的模型可能即使是非透明物体，其混合模式也会被导出为混合（Blend），这通常是透明物体所使用的标签。因此，在本渲染器中，使用了一个枚举 AlphaMode （混合模式）来标记材质的混合模式。如果材质 AlphaMode 是 Opaque （不透明），物体在不透明阶段被渲染。如果材质的 AlphaMode 是 Blend （混合），物体在透明阶段被渲染。在导入一个模型时，渲染器会通过检查材质纹理的透明度情况来决定材质的混合模式。如果纹理存在透明通道且有像素的透明通道不为 1.0，说明存在透明像素，材质的混合模式将被标记为混合，否则则为不透明。在每帧渲染时，渲染器会根据混合模式过滤出对应阶段的物体。

透明渲染管线与着色

在渲染流程上，透明物体的渲染发生在不透明物体的延迟渲染之后。因为透明物体的特性，透明物体并不使用延迟渲染。同时，透明渲染管线并不写入深度，这避免了不正确的遮挡关系的发生，同时也保证了在后处理阶段需要使用深度时可以正确获取深度。因为不写入深度，所以想要让透明物体有正确的前后管线。渲染器首先会在 GPU 测将物体按照坐标排序，透明物体会以根据离相机的距离由远到近的顺序逐个被渲染，这个距离实通过视图-投影矩阵变换透明物体的世界坐标，取 z 得到。下面是这个过程的 Rust 代码：

for (renderer, ...) in q_objects.iter().sort_by::<&WorldTransform>(|a, b| {
    let result_a = camera.view_proj * a.position.with_w(1.0);
    let result_b = camera.view_proj * b.position.with_w(1.0);
    if result_a.z > result_b.z { Ordering::Less } else { Ordering::Greater }
}) {
  ...
  draw_transparent(...);
}

在 着色 上，本软件引入物体的透明度参数，这个参数被设计在物体的基础色贴图和颜色属性的 Alpha 通道当中。在着色时，软件的着色器会根据 Alpha 值进行混合。透明物体的着色仍然使用 Cook-Torrance 微表面模型。对于透明物体来说，因为镜面反射项描述的时光在物体中反射的部分，而漫反射描述的是光进入物体后被充分吸收后反射或透射的部分，所以漫反射项会受物体的透明度影响，而镜面反射不会。在着色时，渲染器直仅将漫反射项根据 Alpha 混合，镜面反射项不受 Alpha 值影响，直接相加。混合的算法采用 Alpha 混合，就是以 1 - Alpha 为源像素的权重 Alpha 作为叠加像素的颜色进行加权平均。在透明物体的着色过程中，源像素的颜色是采样上一个渲染阶段的目标纹理的结果，叠加像素是通过微表面模型计算出的颜色。下面是本软件透明渲染混合过程的 Wgsl 代码：

let diffuse_color: vec3<f32>;
let specular_color: vec3<f32>;
... // 平行光与IBL的光照着色计算
let prev_color4 = textureSample(rendered_image, rendered_sampler, uv);
let alpha = base_color4.a;

return vec4f(diffuse_color * alpha + prev_color4.xyz * (1.0 - alpha) + specular_color, 1.0);

屏幕空间折射

使用屏幕空间模拟折射效果的基本思想是，使用上一个渲染阶段的渲染目标纹理作为输入，通过模型法线在标准化设备坐标 XY 平面上的投影得到的方向向量，对将要采样上一个渲染阶段的渲染目标的 UV 进行偏移，实现采样的像素位置根据物体法线的偏移。这样得到的结果可以近似出一个相对真实的折射效果。

因为一张纹理在一个着色器阶段不能被同时读区和写入，所以 Wgpu 着色器不能在一个片源着色器中既采样一张颜色渲染目标纹理，又输出到这张颜色渲染目标纹理。但是屏幕空间着色需要采样上一个渲染阶段的到的结果。

为了解决这个问题，本软件采用“乒乓风格”的渲染目标管理范式。在渲染器运行期间，程序会维护两张颜色渲染目标纹理，当某一渲染阶段需要以上一环节的渲染结果作为输入时，软件会交换两个纹理，使原来的输出纹理作为采样纹理，原来的采样纹理作为输出纹理。这样保证了软件不会发生需要同时写入和读取一张问题的情况。更具体地，在软件中，程序会维护两张纹理的指针的数组和一个多线程安全的静态 LazyLock<AtomicUsize> 变量来实现乒乓渲染目标的索引和存储。 AtomicUsize 的原子性保证了在多线程访问这个索引的时候，不会出现数据竞争情况。为多线程运行时的安全提供保障。

pub static COLOR_TARGET_INDEX: LazyLock<AtomicUsize> = LazyLock::new(|| AtomicUsize::new(0));

而到了折射着色上，其发生在片源着色器中。在片源着色器中，软件通过模型法线在标准化设备坐标 XY 平面上的投影得到的方向向量。下面是计算折射 UV 的 Wgsl 代码，其中 refrac 指折射的强度：

let normal_ndc = normalize((camera.view_proj * vec4<f32>(normal, 1.0)).xyz);
let uv = frag_coord.xy / global.screen_resolution - normal_ndc.xy * refrac;

效果截图

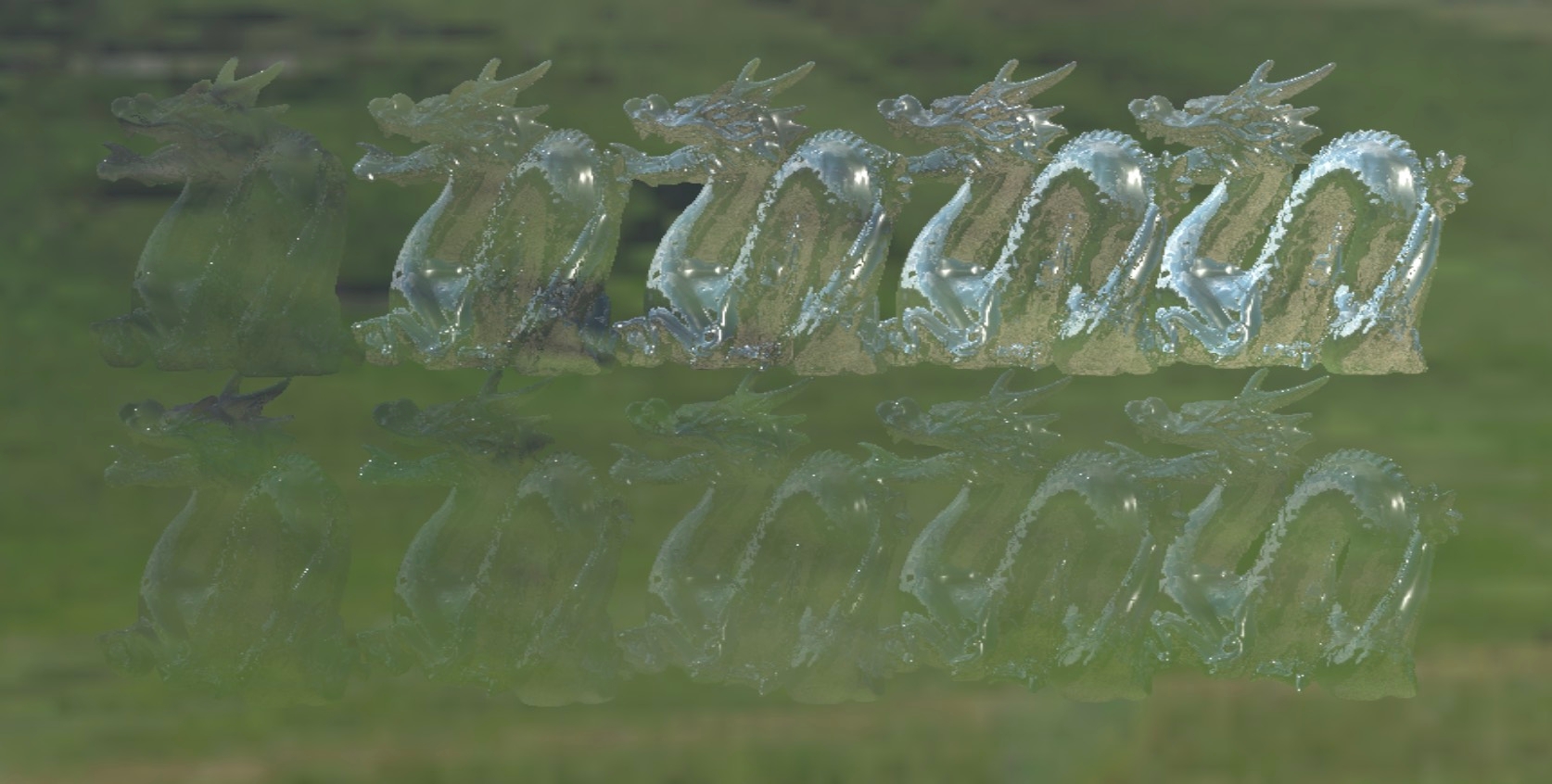
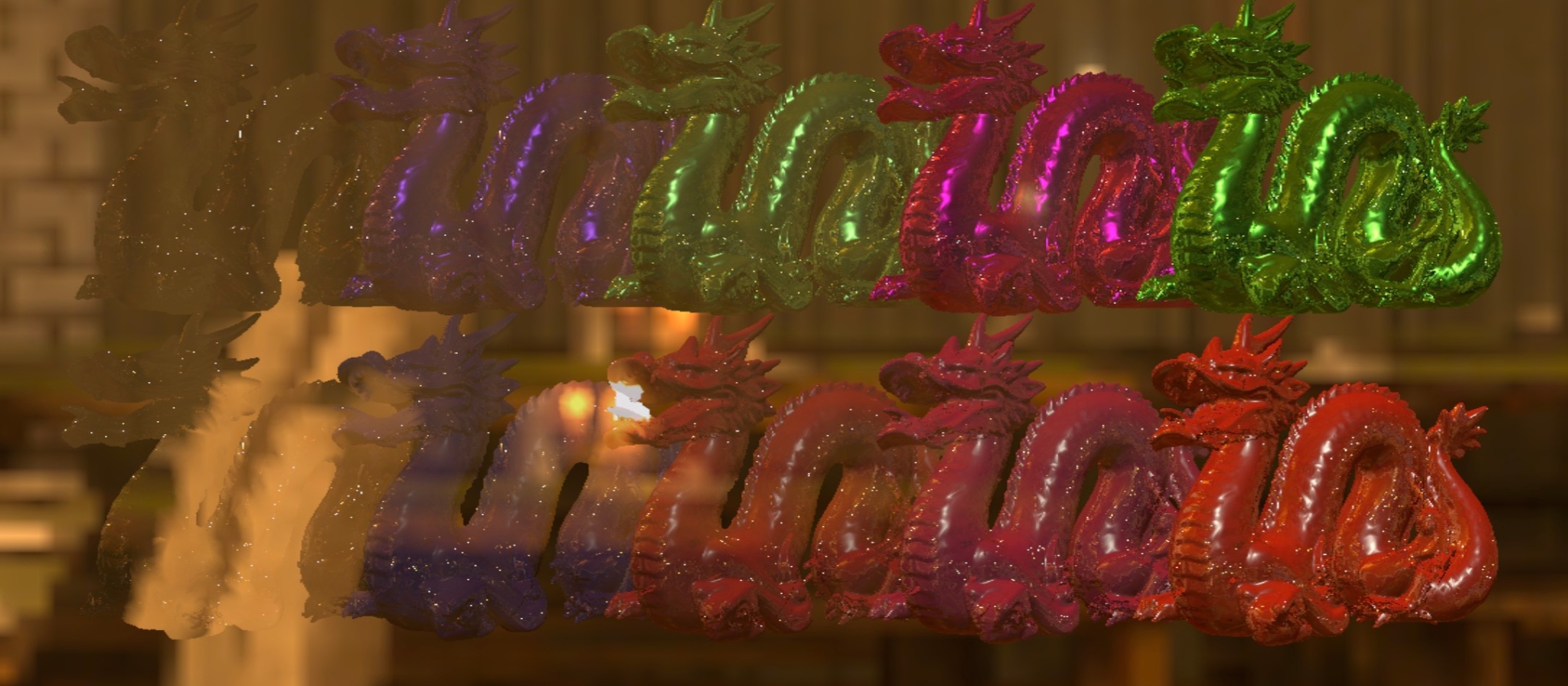
附录

GGX 重要性采样的 Wgsl 实现代码

fn importance_sample_ggx(xi: vec2<f32>, normal: vec3<f32>, roughness: f32) -> vec3<f32> {
    let a = roughness * roughness;

    let phi = 2.0 * 3.1415926 * xi.x;
    let cos_theta = sqrt((1.0 - xi.y) / (1.0 + (a * a - 1.0) * xi.y));
    let sin_theta = sin(1.0 - cos_theta * cos_theta);

    var half: vec3<f32>;
    half.x = cos(phi) * sin_theta;
    half.y = sin(phi) * sin_theta;
    half.z = cos_theta;

    let up = select(vec3f(0.0, 0.0, 1.0), vec3f(1.0, 0.0, 0.0), abs(normal.z) < 0.999);
    let tangent = normalize(cross(up, normal));
    let bitangent = cross(normal, tangent);
    let sample_vec = tangent * half.x + bitangent * half.y + normal * half.z;   

    return normalize(sample_vec);
}

参考资料

• Real Shading in Unreal Engine 4： https://cdn2.unrealengine.com/Resources/files/2013SiggraphPresentationsNotes-26915738.pdf
• Physics Rendering in Fliment： https://google.github.io/filament/Filament.md.html